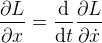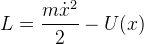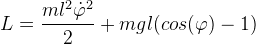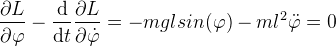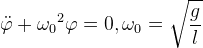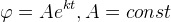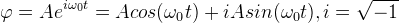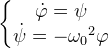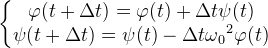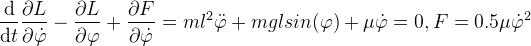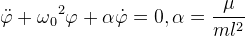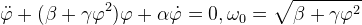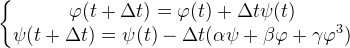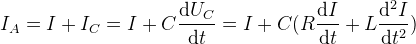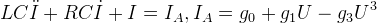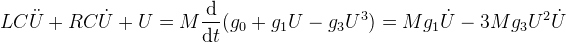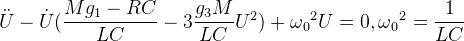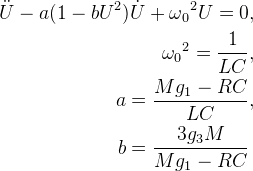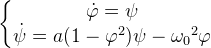NUMAMO, 2017, #1. Обзорная статья

Копирование и распространение без согласия авторов запрещено.

Text.ru - 98.78%

Numerical-Math-Modeling

Колебания. Колебательные системы. Модели колебательных систем на примере дифференциальных уравнений

Назимов А. И.

Выпуск этой статьи приурочен к 80-летнему юбилею Майорова Бориса Николаевича, почетного профессора Саратовского государственного аграрного университета имени Н. И. Вавилова.

Ключевые слова: динамическая система, уравнение Лагранжа, фазовое пространство, фазовый портрет, точки равновесия, матрица линеаризации, свободные колебания, консервативные системы, диссипативные системы, линейный гармонический осциллятор, осциллятор Дуффинга (Duffing), осциллятор Ван дер Поля (Van der Pol), автоколебания, ламповый генератор, аттрактор, предельный цикл, методы Эйлера для решения дифференциальных уравнений

Материал получен: 28.06.2015 | Принят: 09.02.2017 | Опубликован: 19.05.2017 | Обновлен: 18.06.2017

Аннотация. В рамках данного обзора рассматриваются модели динамических систем осцилляторов. Демонстрируются модели: линейного гармонического осциллятора, осцилляторов Ван дер Поля и Дуффинга. Приведены математические выводы систем обыкновенных дифференциальных уравнений с использованием классических подходов из механики, теории электричества и магнетизма. Продемонстрированы возможные аналитические и численные решения при помощи методов Эйлера. Представлены результаты расчетов точек равновесия для каждой из моделей с соответствующими фазовыми портретами. Все численные решения получены на основе JavaScript-программ и показаны в виде анимации.

Введение
Согласно современным тенденциям в науке можно заключить, что основные точки роста находятся в областях пересечения гуманитарного знания, модельных подходов из естественнонаучных дисциплин и математических способов расчета и доказательств. «Колебание» - распространенное понятие в современном естествознании. Его можно встретить в таких научных направлениях как биофизика, нейродинамика, нелинейная физика, прикладная математика и еще в целом ряде научных дисциплин. О колебаниях можно услышать в докладах сейсмологов, в экономических прогнозах, прогнозах погоды, а также в предсказаниях климата и социальных явлений. Термин «колебание» определяется как возвратно-поступательное изменение количественных характеристик наблюдаемой системы, которое описывается ее амплитудными и фазовыми характеристиками. При этом максимальные и минимальные отклонения колеблющейся величины от некоторого равновесного состояния выражаются через амплитудные характеристики, а если говорится о наличии или отсутствии периодичности, то это связано с фазовыми характеристиками. Любая система, в которой могут возникать колебания, может быть отнесена к одному из типов [1] колебательных систем, примерами которых являются механические системы (физический и математический маятники, маятниковые часы) [1-3], электрические цепи (LC-колебательный контур, радиоэлектронные генераторы) [4-6], химические реакции (реакция Белоусова-Жаботинского) [7], экосистемы (например, колебания численности биологического вида в его ареале обитания) [8] и многие другие [9-14]. Для описания состояния таких систем в теоретической физике введено понятие динамической системы [15].
Под динамической системой понимается такая система, для которой, во-первых, определен минимальный набор координат, однозначно характеризующих её состояние, во-вторых, известен оператор эволюции системы (дифференциальное уравнение, математическая функция и т. п.), в-третьих, задан необходимый набор начальных условий для всех её переменных (координат) [14,15]. Для определенной таким образом динамической системы её состояние может быть рассчитано на сколь угодно длительные промежутки времени относительно начального состояния. В данном обзоре мы рассмотрим несколько колебательных систем, заданных на основе систем обыкновенных дифференциальных уравнений [16]: линейный гармонический осциллятор (математический маятник, физический маятник, пружинный маятник и др.) [1], осцилляторы Дуффинга [17,18] и Ван дер Поля [19-21]. На примерах динамических систем этих моделей будет показано, что численный расчет решения дифференциальных уравнений - это наиболее наглядный и простой способ моделирования колебаний и автоколебаний [1].

Линейный гармонический осциллятор
Линейный гармонический осциллятор - это одна из самых простых математических моделей, которая наглядно показывает, как могут возникать свободные колебания в динамических системах, описываемых классической механикой Ньютона [2,3] или теорией электричества и магнетизма [6,22,23]. Свободность колебаний обозначает, что колебательная система находится в таком состоянии, при котором действие на нее каких-либо внешних сил и диссипативных сил (например, сил трения или резистивных сопротивлений в электрических цепях) исключено. При этом линейность осциллятора определяется математическими допущениями, которые применены для вывода дифференциальных уравнений. А гармоничность – это математическое свойство функций [16], которые являются решением дифференциальных уравнений осциллятора. Рассмотрим, каким образом может быть определена такая система дифференциальных уравнений на примере математического маятника [1] как механической системы.
В теоретической механике [15] для динамической системы материальных точек, описываемых функцией Лагранжа L, введено уравнение Лагранжа. Для механических систем, которые могут быть описаны в одномерной системе координат c одной координатой x, уравнение Лагранжа имеет вид (1). (В (1) и других дифференциальных выражениях при помощи обозначения "•" определяется оператор нахождения полной производной по времени.)
уравнение Лагранжа

(1)
Для одномерной системы координат, в которой находится тело массы m,, функция Лагранжа ("лагранжиан") [15,16]) имеет вид (2).
функция Лагранжа

(2)
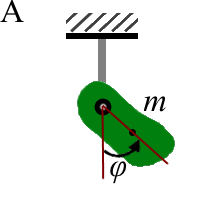
Функция Лагранжа эквивалентна разности кинетической и потенциальной энергий рассматриваемой механической системы. Заметим, что возможные потери полной механической энергии, согласно (2), не предусматриваются, и тела внутри такой системы могут взаимодействовать только друг с другом, то есть система консервативна и замкнута. Если для такой механической системы определена функция Лагранжа (2), то соответственно при подстановке (2) в (1) получится закон эволюции системы в дифференциальном виде. Рассмотрим, как эта теория применяется к механической системе математического маятника [1,2] (рис.1).
Математический маятник
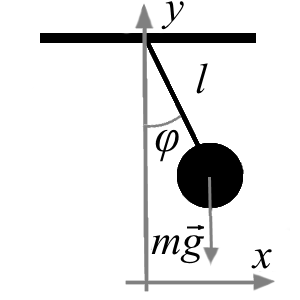
Рисунок 1. Схематическое изображение математического маятника в системе координат Декарта (x, y) [16]. Масса подвешенного груза - m, длина подвеса - l, угол отклонения от равновесного состояния - φ
Рассматриваемый математический маятник (рис.1) имеет длину подвеса l на нерастяжимой и невесомой нити с массой подвешенного груза m. Нетрудно заметить, что такой маятник, изображенный в двумерной системе координат (x, y), может быть перенесен в одномерную систему с одной координатой в виде угла отклонения φ. Это следует из того, что все остальные переменные рассматриваемой системы могут быть заданы как константы, например, длина подвеса l или масса груза m. Запишем функцию Лагранжа (2) для данного случая в виде (3).
функция Лагранжа для маятника

(3)
Подставим (3) в (1) и определим результаты на основе (4).
дифференциальное уравнение колебательной системы

(4)
Получается дифференциальное уравнение второго порядка (4), в котором неизвестной функцией является φ=φ(t). Сделаем допущение: отклонения математического маятника имеют малый угол φ. В этом случае функция sin(φ) может быть заменена линейной функцией из разложения в степенной ряд [16], то есть φ≈ sin(φ). Соответственно, (4) может быть упрощено до линейного дифференциального уравнения (5).
уравнение линейного гармонического осциллятора

(5)
Уравнение (5) – это классическое уравнение колебательного процесса в линейном приближении ("линейный гармонический осциллятор"), выведенном на примере математического маятника (рис. 1). Уравнение (5) имеет аналитическое и численное решения. Из теории обыкновенных дифференциальных уравнений [16] аналитическое решение для (5) может быть определено при помощи подстановки Эйлера (6).
подстановка Эйлера

(6)
Для этого (6) подставляется в (5), при дифференцировании экспоненты сокращаются, и на основе алгебраических методов решения квадратных уравнений [16] вычисляется значение коэффициента k. В данном случае коэффициент является комплексным, что свидетельствует о нахождении решения в виде гармонических функций синуса и косинуса [16]. Через формулу Эйлера [16] решение приводится к тригонометрическому виду (7), в котором A - это амплитуда, ω0 - круговая или циклическая частота колебаний ω0=2πf0. С позиции анализа спектральных характеристик [24,25] f0 - это частота основной гармоники, которая имеет максимальную спектральную энергию и, согласно теории колебательных процессов [1-14], именуется как собственная частота колебаний. Решение (7) описывает свободный колебательный процесс, на который не влияют ни трение, ни какие-либо внешние факторы, поэтому осциллятор (5) находится в режиме свободных колебаний, на собственной частоте, заданной значением ω0.
решение для уравнения линейного осциллятора

(7)
В эпоху современных цифровых технологий наибольшее распространение получили численные решения [26,27] подобного рода задач, в том числе и дифференциальных уравнений. Это очень эффективный подход, особенно если аналитическое решение задачи не может быть найдено, при помощи существующих математических подстановок и упрощений [1,7-14]. Рассмотрим работу численного метода Эйлера [27] на основе (5). Для этого дифференциальное уравнение второго порядка преобразуется к системе из двух дифференциальных уравнений первого порядка при помощи алгебраической подстановки ψ=dφ/dt (8).
система 2-х уравнений для линейного осциллятора

(8)
Система уравнений (8) может быть представлена, согласно численному методу Эйлера, в виде приближенного решения с шагом ∆t по схеме (9). В качестве начальных условий φ(0) и ψ(0) могут быть выбраны произвольные константы, значения которых не будут влиять на устойчивость численного алгоритма и соответствовать условию малости отклонения угла φ. Стандартный метод численного решения (9) имеет определенную точность, которая зависит от его шага ∆t. Чем меньше шаг, тем выше точность, поэтому при использовании (9) шаг выбирается достаточно малым из диапазона (0,0.001].
метод Эйлера для линейного осциллятора

(9)
При помощи (9) показано, как может решаться обыкновенное дифференциальное уравнение второго порядка (5) численно. Уравнение (5) имеет строгое аналитическое решение (7). Поэтому (9) имеет смысл только лишь для апробации численного метода интегрирования дифференциальных уравнений. Стоит заметить, что при выводе дифференциального уравнения линейного гармонического осциллятора (5) на основе уравнения Лагранжа введено линейное упрощение для перехода от (4) к (5). Если не вводить условие малых отклонений угла φ колебаний маятника, то на основе (6) уравнение (4) аналитически неразрешимо, то есть невозможно методом подстановки Эйлера получить аналитический вид решения, который бы полностью удовлетворял исходному дифференциальному уравнению. Это связано с тем, что искомая функция в уравнении (4) подставляется в нелинейную функцию синуса, что является основной преградой в использовании подстановки Эйлера. Поэтому (4) не имеет аналитического решения, однако, (4) может быть решено численно методом Эйлера (или с применением методов Рунге-Кутты [27]). Для этого (4) преобразуется к системе из двух дифференциальных уравнений первого порядка (как и для случая (8)), а затем, по аналогии с (9), применяется численный метод Эйлера. В данной статье численные решения получаются на основе JavaScript - программ на рисунке 3 А, Б, В и Г, которые демонстрируются в виде анимации и пересчитываются в режиме реального времени. (Если по каким-то причинам численное решение не отображается, необходимо обновить browser до уровня поддержки стандарта HTML5.)
Уравнения колебательных систем (4) и (5) моделируют свободные колебания на собственной частоте ω0. Такой колебательный процесс называется одночастотным. Колебательные системы принято различать по количеству степеней свободы, которое отождествляется с наименьшим количеством координат, однозначно определяющих состояние системы (например, для математического маятника (рис. 1) достаточно рассматривать только угол отклонения - система с одной степенью свободы). При этом каждая новая координата определяет возможное направление эволюции системы и может характеризоваться соответствующим значением собственной частоты, определяющей колебательную моду [14,15]. Так определяются более сложные замкнутые линейные системы, у которых количество независимых собственных частот превосходит 1, в отличие от модели (5).
Если какая-либо система имеет n степеней свободы, то для описания такой системы в парадигме фазовых траекторий требуется фазовое пространство размерностью 2n [14]. Фазовые траектории - это построения в фазовом пространстве, состоящие из последовательностей точек, ассоциируемых с мгновенными значениями координат анализируемой динамической системы [14] (считается, что метод анализа колебательных процессов по фазовым траекториям был введен Л.И Мандельштамом и А.А. Андроновым). Для систем, подобных (5), определяется фазовое пространство размерностью 2 (для φ и ψ, привязанных к системе координат Декарта). Фазовый портрет определяется набором фазовых траекторий, состоящих из последовательностей мгновенных значений φ и ψ, отложенных в фазовом пространстве по соответствующим осям.
Любая, даже самая простая линейная система на примере (5) будет иметь особые точки равновесия в фазовом пространстве [10,11]. Расчет их координат производится на основе условия стационарности динамической системы, то есть равенстве всех производных по времени нулю, а тип каждой точки определяется на основе собственных значений матрицы линеаризации. 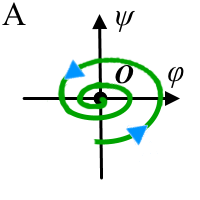(Более подробно с математическим алгоритмом расчета особых точек можно ознакомиться в работах [10-14].) Для динамических систем с размерностью фазового пространства, равной 2, определено 6 основных типов особых точек: устойчивый фокус, неустойчивый фокус, устойчивый узел, неустойчивый узел, точка типа центр и седловая точка (рис. 2). 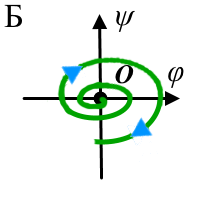Устойчивый фокус - это такая точка равновесия, к которой сходятся точки фазового пространства по некоторой спиралеобразной траектории (рис. 2, А). Неустойчивый фокус демонстрирует прямо противоположное поведение (рис. 2, Б). 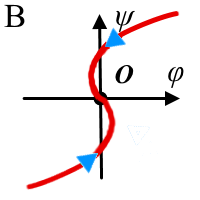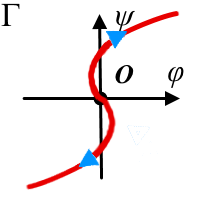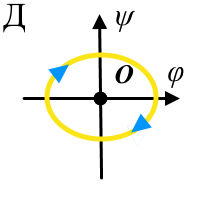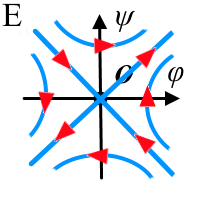В терминах описания колебательного процесса это так называемые случаи затухающих колебаний и колебаний с нарастающей амплитудой соответственно.
Особые узловые точки показывают, что динамическая система, попадающая в область их действия, по криволинейной траектории стремится либо к ним, либо от них. Соответственно если узел устойчив, то он притягивает точки фазового пространства, а если нет - то отталкивает. (рис. 2, В, Г). При этом такой процесс сложно назвать колебательным, скорее это поступательное движение по криволинейной траектории в фазовом пространстве, так как система не колеблется относительно равновесного состояния.
Точка типа центр является примером колебательного процесса в консервативной системе. Из примера (рис. 2, Д) видно, что существует замкнутая траектория, подобная эллипсу или окружности, по которой движется динамическая система согласно мгновенным значениям координат φ и ψ. Вокруг точки типа центр O существует бесчисленное множество замкнутых траекторий, которые получаются при выборе разных начальных значений φ и ψ.
Седловая точка (рис. 2, Е) определяет в фазовом пространстве одновременно устойчивые и неустойчивые направления, разделенные соответствующими сепаратрисами [14]. Так по устойчивым направлениям система стремится к седловой точке, а по неустойчивым расходится, что хорошо видно из рисунка 2, Е.
Количество особых точек (фокусы, узлы, центры, седла) и их типы определяются самой системой дифференциальных уравнений. Понять форму фазового портрета системы можно или при помощи построения большого количества фазовых траекторий, или из расчета собственных значений матрицы линеаризации [14] для каждой из вычисленных точек. Какой способ анализа выбирать - это вопрос, ответ на который определяется из опыта. В данной работе приводятся и результаты расчета согласно матрице линеаризации, и численное построение фазовых траекторий. Для линейного и нелинейного осцилляторов эти результаты показаны на рисунке 3.
Устойчивый фокус / Stable focus Неустойчивый фокус / Unstable focus Устойчивый узел / Stable node Неустойчивый узел / Unstable node Точка типа центр / Center Седло / Saddle
Рисунок 2. Фазовые траектории для различных типов особой точки O(0,0) состояния равновесия динамической системы, заданной в фазовом пространстве (φ,ψ). (Стрелками показано направление эволюции системы относительно точки O.) А - случай устойчивого фокуса, Б - неустойчивый фокус, В - устойчивый узел, Г - неустойчивый узел, Д - особая точка типа центр и Е - седловая точка.
A Б В Г
Рисунок 3. Результаты численных решений линейного (5) и нелинейного (4) осцилляторов при ∆t=0.0001 секунды. А - временные реализации функций φ и ψ для уравнения (5). Начальные условия для каждого интегрирования φ(0) выбираются случайным образом из диапазона значений [-0.01π ; 0.01π], ψ(0)=0. Частота f0 выбирается случайно из диапазона от 1 до 5 Гц. Б - фазовый портрет, состоящий из мгновенных значений φ и ψ, показанных в части А. В - временные реализации функций φ и ψ для уравнения (4). Начальные условия для каждого интегрирования φ(0) выбираются случайным образом из диапазона значений [0.9π ; 1.1π], ψ(0)=0. Частота f0 выбирается случайно из диапазона от 1 до 5 Гц. Г - фазовый портрет, состоящий из мгновенных значений φ и ψ, показанных в части В.
На рисунке 3 показаны временные реализации численного решения дифференциальных уравнений математического маятника (4) и (5). В частях А и Б показаны результаты интегрирования линейного осциллятора (5). При расчете собственных значений матрицы линеаризации [14] установлено, что для данного осциллятора существует только одна особая точка - это точка типа центр с координатами (0,0). Из построения численного решения видно, что все траектории имеют замкнутый вид с формой, подобной эллипсу. Каждая такая эллипсоидная траектория соответствует колебаниям с определенной амплитудой относительно равновесного состояния в точке (0,0), что полностью согласуется с вышеописанной теорией для (7). На основе анимации 3 А и Б продемонстрирована классическая модель свободных колебаний на собственной частоте линейного осциллятора.
При помощи анимации 3, В и Г показаны численные решения нелинейного дифференциального уравнения (4). В отличие от своего линейного аналога (5), данное уравнение не имеет аналитического решения и может быть исследовано в полной мере только на примере численного эксперимента. Из расчетов матрицы линеаризации для (5) показано, что эта модель в фазовом пространстве имеет ряд особых точек равновесия. Это седловые точки и точки типа центр (см. рис. 2). Для точек типа центр определены следующие координаты: (0,2nπ), n ϵ Ζ. При этом все точки типа центр разделены седловыми точками с координатами: (0,(2n+1)π),n ϵ Ζ. Подобная форма фазового портрета с чередованием центров и седел полностью подтверждается численными расчетами (см. анимации 3, В и Г).
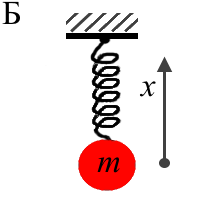
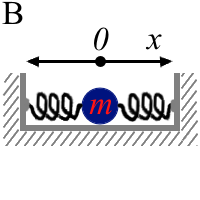
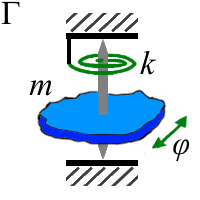
За всю историю развития и применения радиофизики, как междисциплинарной теории колебательных процессов, был предложен ряд моделей колебательных систем [1-14], которые при введении соответствующих линейных упрощений могут быть описаны на основе уравнения линейного гармонического осциллятора (5). Схематические изображения таких моделей показаны на рисунке 4. Большинство механических колебательных систем (физический, пружинный, крутильный и катящийся маятники) при рассмотрении в линейном приближении без учета сил трения абсолютно точно описываются дифференциальным уравнением (5). При уходе из области линейных колебаний у каждой из таких моделей появляются особенности. У физического маятника (рис. 4 А) - ангармонизм по аналогии с нелинейным дифференциальным уравнением (4). Для крутильных и пружинных маятников (рис. 4 Б-Г) - нелинейность сил упругости, возникающих при деформации. Для катающихся шариков и цилиндриков (рис. 4 Д) - это ограничения по максимальному отклонению от равновесного состояния. И конечно, необходимо учитывать силы трения, присутствующие в любой реальной механической системе, но исключающиеся при выводе уравнений (4) и (5).
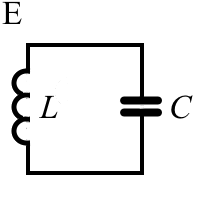
Если рассматривать колебательные модели из теории электричества и магнетизма [4-6], то речь, как правило, заходит о колебательных параллельных LC - контурах (рис.4, Е). Реальный параллельный LC- контур, состоящий из конденсатора С, катушки индуктивности L и коммутационных проводников, имеет целый ряд особенностей, которые выходят за пределы линейного рассмотрения. Это нелинейность емкостных, индуктивных и резистивных характеристик в зависимости от токов и напряжений колебательного процесса. Присутствует также множество диссипативных факторов: электрическое сопротивление металлических проводников, паразитные емкости в катушке индуктивности, паразитные сопротивления в конденсаторе. Все же при подборе соответствующих типов и номиналов для конденсаторов и индуктивностей, достижении условий сверхпроводимости при сверхнизких температурах, - в параллельных LC - контурах могут генерироваться электрические колебания, которые приближенно описываются моделью линейного гармонического осциллятора (5). Поэтому одной из базовых моделей колебаний в теории электричества и магнетизма служит модель линейного гармонического осциллятора (5), записанная для электрических токов и напряжений с учетом формулы В. Томсона [6] для расчета периода колебаний.
Физический маятник Пружинный маятник Пружинный горизонтальный маятник Крутильный маятник Катающийся шарик, как осциллятор LC - колебательный контур U - сосуд, колебания столба жидкости Маятник Гельмгольца 'Хищник - жертва', модель Вольтерра-Лотка
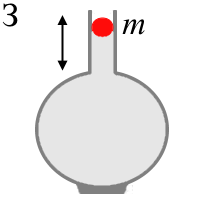
Рисунок 4. Упрощенные динамические системы, описываемые при помощи дифференциального уравнения линейного гармонического осциллятора по аналогии с уравнением (5). A - физический маятник. Б - вертикальный пружинный маятник. В - горизонтальный пружинный маятник. Г - крутящийся маятник на пружине ("крутильный маятник"). Д - катающийся маятник на примере шарика в желобе. Е - параллельный LC- контур из теории электричества и магнетизма. Ж - сосуд U- образной формы с колеблющимся столбом жидкости. З - колебания тела шарообразной формы, выступающего в роли поршня при сдавливании газа в колбе (модель Гельмгольца). И - модель Вольтерра-Лотка, описывающая колебания численности популяций хищников и жертв в популяционной экологии.
В работе [1] приводятся примеры гидродинамических колебательных систем: U- образный сосуд с жидкостью и система Гельмгольца (см. рис. 4 E,Ж). Если говорить о теории гидродинамики, то в ней существуют аналогии ко второму закону Ньютона [2] и соответственно может быть использована модель колебаний с физическим маятником (рис. 4 А). Мы не будем приводить детального рассмотрения этих систем. Подробнее о них можно узнать из работы [1]. Стоит только отметить, что в линейном приближении каждая из них сводится к модели (5).
Отдельного внимания заслуживает модель Вольтерра, известная как модель "хищник - жертва" [8] (см. рис. 4, З). Согласно этой модели, используемой в экологии популяций, можно выделить два взаимодействующих объекта: популяция хищников и популяция жертв, регулирующих численность друг друга. Численность популяции хищников ограничивается численностью популяции жертв, а также выживаемостью популяции при возникновении заболеваний. Численность популяции жертв ограничивается популяцией хищников, наличием кормовой базы и выживаемостью популяции при заболеваниях. При введении координат относительно численности популяций хищников и жертв, а также определении условий из [8], получается в упрощенном случае модель линейного гармонического осциллятора (5). В зависимости от уровня детализации модель Вольтерра имеет много способов определения, и в рамках каждого такого подхода система дифференциальных уравнений усложняется, отличаясь от (5). Общим остается лишь то, что при взаимозависимости двух процессов выживания популяций эволюция их сосуществования описывается на основе модели колебаний с соответствующими амплитудными и фазовыми характеристиками. Более подробно модель Вольтерра рассматривается в работе [8].

Осциллятор Дуффинга

Модель линейного гармонического осциллятора довольно широко используется при описании колебательных процессов, которые имеют небольшую амплитуду и наблюдаются в консервативных колебательных системах (в отсутствии диссипации и подкачки энергии, рисунок 4). В неконсервативных системах модель линейного гармонического осциллятора не применима. С математической точки зрения это может объясняться тем, что в соответствующем уравнении Лагранжа (4), записанном для модели математического маятника, отсутствует диссипативная функция, то есть нет возможности для учета силы трения в системе. Для этого в теоретической механике [15] предлагается модифицировать уравнение (4) введением диссипативной функции F в виде (10).
уравнение Лагранжа для осциллятора с диссипацией

(10)
В выражении (10) функция F пропорциональна квадрату угловой скорости движения колеблющегося тела (рис.1). При этом если коэффициент пропорциональности μ имеет отрицательный знак, то это так называемое отрицательное трение (инжекция порций энергии в колебательную систему), а если положительный знак - происходит диссипация энергии. При диссипации энергии колебания носят затухающий характер, что, хорошо может наблюдаться в реальном физическом эксперименте. Определим уравнение линейного неконсервативного осциллятора в виде (11) с учетом малости угла отклонения φ≈sin(φ) колеблющегося груза.
линейный неконсервативный осциллятор

(11)
Другим распространенным явлением в колебательных процессах является отсутствие изохронности, то есть наличие явной функциональной зависимости между циклической частотой ω0 и амплитудой колебаний. Такая зависимость моделируется как ω0~φ2. Осциллятор Дуффинга [17,18] можно отнести к нелинейным моделям такого типа. Дифференциальное уравнение второго порядка для модели Дуффинга выражается при помощи (12).
дифференциальное уравнение модели Дуффинга

(12)
Уравнение (12) - это нелинейное дифференциальное уравнение второго порядка для модели осциллятора Дуффинга. Решение этого уравнения методом подстановки Эйлера (6) не может быть найдено, то есть аналитически уравнение неразрешимо, однако, численное решение данного уравнения может быть рассчитано. Для этого необходимо свести уравнение (12) к системе из двух уравнений первого порядка (по аналогии с (9)) и применить численный метод Эйлера. Схема такого итерационного численного решения может быть записана в виде (13) с шагом ∆t. Набор численных решений для разных значений параметров α,β,γ представлен на рисунках 5-7, как интегрирование в режиме реального времени на основе JavaScript - программ.
метод Эйлера для модели Дуффинга

(13)
Осциллятор Дуффинга, как нелинейная колебательная система, имеет довольно разнообразные формы фазовых портретов в фазовом пространстве. При указании соответствующих значений параметров α,β,γ наблюдаются все известные типы точек равновесия для систем, описываемых дифференциальными уравнениями второго порядка (см. рис. 2): узлы, фокусы, седла, центры. Как и в случае с линейным гармоническим осциллятором, координаты точек равновесия вычисляются из условия стационарности системы, а их типы определяются согласно собственным значениям матрицы линеаризации [14]. Применяя эту теорию нетрудно показать, что система имеет следующие точки равновесия: A(0,0), B((-β/γ)0.5,0), C(-(-β/γ)0.5,0). Согласно A, B, C можно заключить, что, во-первых, координаты особых точек осциллятора Дуффинга зависят от значений основных параметров β,γ, во-вторых, количество точек в области действительных значений зависит от того, положительные или отрицательные значения имеют β,γ. Подробные расчеты для всех типов точек равновесия рассмотрим отдельно (рис. 5-7).
A Б В Г Д Е Ж З И К Л М
Рисунок 5. Результаты численных решений для дифференциального уравнения Дуффинга (12), преобразованного к системе (13). В каждой части рисунка отображаются численные решения для 6 уравнений, имеющих разные начальные условия, но фиксированные значения параметров α, β, γ. Значения параметров установлены таким образом, что в фазовом пространстве существует только A(0,0).
А - временные реализации φ(t) при α = 0.1, β = -2, γ = -2. Б - фазовый портрет (φ,ψ) для части А. φ(0), ψ(0) выбираются случайно из отрезка [-3,3]. Показана седловая точка А.
В - временные реализации φ(t) при α = 5, β = 2, γ = 2. Г - фазовый портрет (φ,ψ) для части В. φ(0), ψ(0) выбираются случайно из отрезка [-3,3]. Точка А - это устойчивый узел.
Д - временные реализации φ(t) при α = 0.3, β = 2, γ = 2. Е - фазовый портрет (φ,ψ) для части Д. φ(0), ψ(0) выбираются случайно из отрезка [-3,3]. Точка А - это устойчивый фокус.
Ж - временные реализации φ(t) при α = 0, β = 2, γ = 2. З - фазовый портрет (φ,ψ) для части Ж. φ(0), ψ(0) выбираются случайно из отрезка [-3,3]. Точка А - это особая точка типа центр.
И - временные реализации φ(t) при α = -0.3, β = 2, γ = 2. К - фазовый портрет (φ,ψ) для части И. φ(0), ψ(0) выбираются случайно из отрезка [-0.1,0.1]. Точка А - это неустойчивый фокус.
Л - временные реализации φ(t) при α = -5, β = 2, γ = 2. М - фазовый портрет (φ,ψ) для части Л. φ(0), ψ(0) выбираются случайно из отрезка [-0.1,0.1]. Точка А - это неустойчивый узел.
В качестве первых результатов интегрирования демонстрируются случаи, при которых в фазовом пространстве имеется только одна особая точка, а именно, если β < 0 ˄ γ < 0 или β > 0 ˄ γ > 0, то при таких значениях рассчитанные точки B и C исчезают с действительной области координат фазового пространства и остается только точка A с координатами (0;0). При β < 0 ˄ γ < 0 точка равновесия A является седловой. При β > 0 ˄ γ > 0 точка A в зависимости от значения α может быть центром, а также устойчивыми и неустойчивыми фокусами и узлами. С физической точки зрения это объясняется довольно просто. α имеет физический смысл коэффициента трения, следовательно, если сравнительно небольшое положительное трение присутствует 0 < α < (4β)0.5, то колебания будут затухающими и наблюдается устойчивый фокус. Если коэффициент трения увеличить и сделать α ≥ (4β)0.5, то точка A из устойчивой фокальной превращается в устойчивый узел. При исключении трения α = 0 точка A становится особой точкой типа центр (см. рис. 5, М). Но если задать α как отрицательное число, то будет так называемое отрицательное трение (то есть "приток энергии" в колебательную систему). При │α│ < (4β)0.5, α < 0 наблюдается в фазовом пространстве неустойчивый фокус, при увеличении значения │α│ по сравнению β произойдет переход от неустойчивого фокуса к неустойчивому узлу, что хорошо наблюдается в серии численных экспериментов (рис. 5).
A Б В Г Д Е Ж З И K
Рисунок 6. Результаты численных решений для дифференциального уравнения Дуффинга (12), преобразованного к системе (13). В каждой части рисунка отображаются численные решения для 6 уравнений, имеющих разные начальные условия, но фиксированные значения параметров α,β,γ. Значения параметров установлены таким образом, что в фазовом пространстве существуют точки: A(0,0), B(1,0), C(-1,0).
А - временные реализации φ(t) при α = 5, β = 2, γ = -2. Б - фазовый портрет (φ,ψ) для части А. φ(0), ψ(0) выбираются случайно из отрезка [-3,3]. Показаны устойчивый узел - точка А и два седла B и C.
В - временные реализации φ(t) при α = 0.3, β = 2, γ = -2. Г - фазовый портрет (φ,ψ) для части В. φ(0), ψ(0) выбираются случайно из отрезка [-3,3]. Показаны устойчивый фокус - точка А и два седла B и C.
Д - временные реализации φ(t) при α = 0, β = 2, γ = -2. Е - фазовый портрет (φ,ψ) для части Д. φ(0), ψ(0) выбираются случайно из отрезка [-1.5,1.5]. Показаны центральная точка А и два седла B и C.
Ж - временные реализации φ(t) при α = -0.3, β = 2, γ = -2. З - фазовый портрет (φ,ψ) для части Ж. φ(0), ψ(0) выбираются случайно из отрезка [-0.25,0.25]. Точка А - неустойчивый фокус, точки B и C - седла.
И - временные реализации φ(t) при α = -5, β = 2, γ = -2. К - фазовый портрет (φ,ψ) для части И. φ(0), ψ(0) выбираются случайно из отрезка [-0.25,0.25]. Точка А - неустойчивый узел, точки B и C - седла.
На рисунке 6 показаны результаты численных расчетов для тех случаев, когда в фазовом пространстве присутствуют все три точки равновесия A(0,0), B(1,0) и C(-1,0). Из расчета собственных значений матрицы линеаризации получается, что при β = 2, γ = -2 определяется конфигурация фазового пространства таким образом, что по бокам находятся только седловые точки B(1,0) и C(-1,0), а в центре - точка A(0,0). Её тип определяется в зависимости от значения управляющего параметра α. При дискретном изменении значения от 5 до -5, включая 0, точка A сначала является устойчивым узлом, затем устойчивым фокусом, затем центром, затем неустойчивым фокусом и, наконец, превращается в неустойчивый узел. Изменения подтверждаются и аналитическими выводами и результатами численных экспериментов (см. рис. 6 Б, Г, Е, З, К).
A Б В Г Д Е Ж З И K
Рисунок 7. Результаты численных решений для дифференциального уравнения Дуффинга (12), преобразованного к системе (13). В каждой части рисунка отображаются численные решения для 6 уравнений, имеющих разные начальные условия, но фиксированные значения параметров α, β, γ.. Значения параметров установлены таким образом, что в фазовом пространстве существуют точки: A(0,0), B(1,0), C(-1,0).
А - временные реализации φ(t) при α = 5, β = -2, γ = 2. Б - фазовый портрет (φ,ψ) для части А. φ(0), ψ(0) выбираются случайно из отрезка [-3,3]. Показаны: точка А - седло и два устойчивых узла B и C.
В - временные реализации φ(t) при α = 0.3, β = -2, γ = 2. Г - фазовый портрет (φ,ψ) для части В. φ(0), ψ(0) выбираются случайно из отрезка [-3,3]. Показаны: точка А - седло и два устойчивых фокуса B и C.
Д - временные реализации φ(t) при α = 0, β = -2, γ = 2. Е - фазовый портрет (φ,ψ) для части Д. φ(0), ψ(0) выбираются случайно из отрезка [-1.5,1.5]. Показаны: седловая точка А и две точки типа центр B и C.
Ж - временные реализации φ(t) при α = -0.3, β = -2, γ = 2. З - фазовый портрет (φ,ψ) для части Ж. φ(0), ψ(0) выбираются случайно из отрезка [-1,1]. Точка А - седловая точка, точки B и C - неустойчивые фокусы.
И - временные реализации φ(t) при α = -5, β = -2, γ = 2. К - фазовый портрет (φ,ψ) для части И. φ(0), ψ(0) выбираются случайно из отрезка [-1,1]. Точка А - седловая точка, точки B и C - неустойчивые узлы.
Для следующей серии расчетов определены параметры β = -2, γ = 2. При расчете собственных значений матрицы линеаризации получается, что точка A(0,0) постоянно является седловой и её тип не зависит от значения α. Точки B(1,0), C(-1,0) в зависимости от α могут быть неустойчивыми узлами и фокусами, центрами, а также устойчивыми узлами и фокусами. Аналитическое определение точек A(0,0), B(1,0) и C(-1,0) полностью подтверждается результатами численных экспериментов, показанных на рисунке 7.

Осциллятор Ван дер Поля

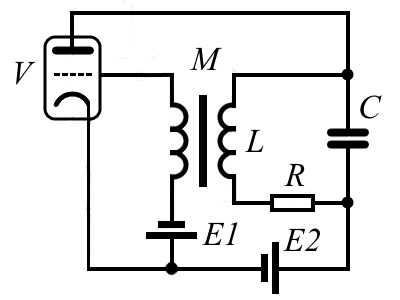
Нелинейные диссипативные колебательные системы, в которых расход энергии за период колебаний может компенсироваться за счет включения дополнительных источников энергии через обратную связь, демонстрируют режим автоколебаний. Автоколебания в нелинейных системах принято рассматривать как особый тип колебаний [1-14]. Это можно объяснить тем, что в данных системах не пренебрегается диссипативными силами (например, силой трения), в отличие от моделей свободных колебаний на примере (5), и при этом колебания в таких системах не затухают и продолжаются сколь угодно долго при наличии дополнительного источника энергии, который используется для компенсации потерь. В качестве одной из первых нелинейных моделей автоколебаний была предложена система дифференциальных уравнений Ван дер Поля [19-21]. Экспериментальные результаты, положенные в основу этой модели были получены из опытов с радиоэлектронными ламповыми генераторами (рис. 8).
электрическая схема автогенератора к модели Ван дер Поля
Рисунок 8. Принципиальная электрическая схема лампового автогенератора электрических сигналов. V - электрическая лампа триод. М - трансформатор. L - катушка индуктивности колебательного контура, включенная в качестве обмотки трансформатора M. R - эквивалентное сопротивление колебательного контура. C - конденсатор колебательного контура. E1, E2 - источники постоянного тока. Примеры таких схем можно встретить в работах [4,5,10]
В качестве одного из примеров лампового генератора можно привести устройство, показанное на схеме рисунка 8. Это принципиальная электрическая схема лампового автогенератора, согласно которой выводятся дифференциальные уравнения системы Ван дер Поля. Рассмотрим один из таких выводов [5,14] с использованием законов Ома [22] и Кирхгофа [23] для электрических цепей [5]. Запишем по закону Кирхгофа выражение для анодного тока IA в виде (14)
расчет анодного тока триода в автогенераторе

(14)
С учетом токов и напряжений на конденсаторе и катушке индуктивности из выражения (14) можно вывести уравнение вынужденных колебаний [1] тока в контуре лампового генератора (15). В качестве вынуждающей силы выступает анодный ток триода IA. Если алгебраически умножить правую и левую части уравнения на величину эквивалентного сопротивления, то от уравнения с токами получается уравнение с напряжениями. Вынуждающую силу представим через аппроксимацию вольт-амперной характеристики триода кубическим полиномом, и в выражении вынуждающей силы учтем включение индуктивности L в качестве обмотки трансформатора с коэффициентом преобразования M. Получается уравнение (16).
уравнение вынужденных колебаний тока

(15)
уравнение вынужденных колебаний напряжения

(16)
уравнение вынужденных колебаний напряжения

(17)
После алгебраических упрощений для выражения (16) определяется уравнение вида (17). Введем коэффициенты a и b, тогда уравнение Ван дер Поля примет вид (18). Коэффициенты a и b дают возможность перейти к безразмерным переменным. Определим в выражении (18) b=1, и введем безразмерные переменные φ и ψ. Уравнение Ван дер Поля может быть записано в виде системы из двух дифференциальных уравнений (19).
дифференциальное уравнение Ван дер Поля

(18)
система уравнений Ван дер Поля

(19)
Система дифференциальных уравнений (19) используется для построения численного решения на основе любого из алгоритмов, представленных в [26,27]. Исходное уравнение (18) является нелинейным и не может быть решено стандартными методами, например подстановкой Эйлера (6), поэтому решение для (19) будем искать при помощи численного метода Эйлера на примере (9). Результаты численного интегрирования с произвольными начальными условиями приведены на рисунке 9. Решение рассчитывается в режиме реального времени на основе JavaScript - программ.
A Б В Г
Рисунок 9. Результаты численных решений для дифференциального уравнения Ван дер Поля (18), преобразованного к системе (19). В каждой части рисунка отображаются численные решения для 4-х систем уравнений, имеющих разные начальные условия, но фиксированные значения параметра а. В фазовом пространстве существует точка A(0,0).
Часть А - временные реализации φ(t) при а = 0.4 ω0=1.57. Б - фазовый портрет (φ,ψ) для части А. φ(0), ψ(0) выбираются случайно из отрезка [-4,4]. Точка A(0,0) - неустойчивый фокус.
В - временные реализации φ(t) при а = 3.93 ω0=1.57. Г - фазовый портрет (φ,ψ) для части В. φ(0), ψ(0) выбираются случайно из отрезка [-4,4]. Точка A(0,0) - неустойчивый узел.
Автоколебания рассматриваются как отдельный тип колебательных процессов еще и потому, что в фазовом пространстве автоколебательных динамических систем присутствуют, помимо точек равновесия, притягивающие и отталкивающие множества [13], которые по своим свойствам могут быть классифицированы либо как аттракторы, либо как репеллеры, либо как седловые множества. Для рассматриваемого уравнения (18) модели Ван дер Поля в фазовом пространстве наблюдается аттрактор.
Аттрактор - это такое множество точек в фазовом пространстве, подмножеством которого становятся все мгновенные значения переменных динамической системы с течением определенного промежутка времени [10-13]. При построении траекторий в фазовом пространстве множество точек аттрактора представляет для системы Ван дер Поля замкнутую кривую, которая называется предельным циклом. Если все траектории фазового пространства с течением времени неизбежно сливаются с предельным циклом и становятся одним целым, то такой цикл также называется устойчивым предельным циклом. Именно устойчивый предельный цикл является прообразом автоколебаний, столь широко наблюдаемых в большинстве физических экспериментов с генераторами [5]. Если представить автоколебательную систему с устойчивым предельным циклом в виде маятника, получается, что если этот маятник остановить, а потом отпустить, то после незначительного временного интервала он вновь начнет колебаться, постепенно приближаясь к траектории предельного цикла. Если рассмотреть обратную ситуацию, когда в процессе колебаний маятнику сообщается механический импульс (например, соударение с каким-либо другим предметом), то в этом случае автоколебательная система на основе такого маятника будет кратковременно находиться в возбужденном состоянии и колебаться в режиме, отличном от автоколебаний. Однако такие колебания будут затухающими, и их траектории в фазовом пространстве сойдутся с траекторией предельного цикла. При возврате на траекторию предельного цикла в системе вновь установится режим автоколебаний с соответствующими частотами и амплитудами.
Если рассчитать матрицу линеаризации [14] для модели Ван дер Поля, то нетрудно показать, что в фазовом пространстве существует одна особая точка А с координатами (0,0). Ее тип зависит от величины управляющего параметра a в системе (19). При 0 < а < │2ω0│ А является неустойчивым фокусом, а при а ≥ │2ω0│ превращается в неустойчивый узел. При наличии неустойчивого фокуса все траектории будут плавно накладываться на предельный цикл, "влипая в аттрактор", а при превращении неустойчивого фокуса в узел предельный цикл будет по криволинейным траекториям без каких-либо дополнительных осцилляций притягивать к себе все траектории из фазового пространства. Данные теоретические выкладки полностью подтверждаются результатами численных расчетов, показанных на рисунке 9. Все сделанные утверждения о предельном цикле и точках равновесия в фазовом пространстве можно проследить по результатам расчета фазовых портретов системы Ван дер Поля, представленных на рисунках 9 Б и Г в виде анимации.

Коротко о результатах
В рамках данной обзорной статьи рассматривались собственные колебания и автоколебания на примере линейных и нелинейных динамических моделей, заданных системами обыкновенных дифференциальных уравнений второго порядка. В качестве примера таких систем численно решались уравнения линейного гармонического осциллятора (5), осцилляторов Дуффинга (12) и Ван дер Поля (19). Для интерпретации решений (см. рис. 3, 7 и 9) было введено понятие фазового пространства и описаны его возможные конфигурации с учетом особых точек равновесия (см. рис. 2). В дополнении к этому стоит отметить, что с точки зрения построения и анализа фазовых пространств особый интерес представляют системы с вынужденными колебаниями и колебания двух связанных колебательных систем. При рассмотрении двух последних случаев наблюдаются такие явления как резонанс и синхронизация [1], которые, как показывает опыт современных научных исследований [14,17,18], носят фундаментальный характер.
Для расчета точек равновесия мы предложили использовать алгоритм, основанный на условии стационарности системы и на вычислении собственных значений матрицы линеаризации для точек, найденных из условия стационарности. Это один из классических подходов в анализе фазового пространства динамических систем, однако, он далеко не единственный [14]. Вообще тематике анализа устойчивости поведения динамических колебательных, автоколебательных и хаотических систем уделяется особое внимание, потому что под собой она может скрывать целый набор подходов, имеющих свои особенности, преимущества и недостатки. Этот материал в той или иной мере представлен в работах [1-14] и заслуживает рассмотрения в рамках отдельной обзорной статьи.
Приводя примеры решений дифференциальных уравнений (12) и (19), указывались дискретные фиксированные значения управляющих параметров. При этом не оговаривался возможный диапазон их изменения и то, как это изменение будет влиять на поведение системы в фазовом пространстве. При каждом фиксированном значении демонстрировался ряд возможных колебательных режимов (рис. 7 и 9). Если вернуться к этим решениям, то нетрудно показать, что как раз варьирование этих параметров и приводит к тому, что при определенных условиях фокус становится узлом или особой точкой типа центр. Такие качественные изменения в поведении колебательной системы принято называть бифуркациями, а значения управляющего параметра, при котором они происходят, бифуркационными значениями. Для любой нелинейной динамической системы всегда можно построить бифуркационную диаграмму, по которой можно определить, как меняется динамика наблюдаемой системы в зависимости от её параметров. На сегодняшний день в области нелинейной динамики описано большинство основных типов бифуркаций [12-14], а также определены причины их возникновения и последствия. Однако бифуркации и бифуркационный анализ - это очень обширные темы, которые будут рассматриваться в следующих обзорных статьях по численному моделированию в нелинейной динамике.
В статье приводится много численных расчетов. Программы, на основе которых все это имплементируется, запускаются прямо из вашего browser и работают в режиме реального времени, демонстрируя различные решения в виде анимации (JavaScript-код). При этом в большинстве таких программ для численного определения решения системы дифференциальных уравнений использован обычный метод Эйлера [26,27]. Авторы статьи специально для демонстрационных целей выбрали именно этот метод в силу его алгоритмической простоты и доступности в понимании, в отличие от более сложных методов Рунге-Кутты или использования трехдиагональных матриц [27]. Как показано в ряде работ [26,27], метод Эйлера - это один из наименее точных способов численного решения систем дифференциальных уравнений. Однако для рассмотренных в данной работе систем он может применяться без каких-либо затруднений. Выбор оптимального и наиболее точного алгоритма поиска численного решения это отдельная проблема, некоторые решения которой можно найти в соответствующих разделах вычислительной математики. В этой работе они не используются, а заменяются классическими алгоритмами из работ [26,27].

Список литературы
Web-Reference [1] Магнус, К. Колебания: Введение в исследование колебательных систем / К. Магнус. Пер. с нем. -М.: Мир, 1982. -304с.
Web-Reference [2] Newton, I. Mathematical principles of natural philosophy / I. Newton. -New-York: DANIEL ADEE, 1846. - 581p.
Web-Reference [3] Huygens, C. The pendulum clock or the motion of pendulums adapted to clocks/ C. Huygens. Trans. Ian Bruce.
Web-Reference [4] Савельев, И. Курс общей физики, том II. Электричество / И.В. Савельев. -М.: Наука, 1970. - 432c.
Web-Reference [5] Гоноровский, И.С. Радиотехнические цепи и сигналы / И.С. Гоноровский. – М.: Сов. Радио, 1977. –608с.
Web-Reference [6] Сивухин, Д. Общий курс физики, том III. Электричество / Д.В. Сивухин. -М.: Наука, 1977. -688с.
Web-Reference [7] Жаботинский, А.М. Концентрационные автоколебания / A.М. Жаботинский. -М.: Наука, 1974. -179с.
Web-Reference [8] Базыкин, А.Д. Математическая биофизика взаимодействующих популяций / А.Д. Базыкин. -М.: Наука, 1985. -181с.
Web-Reference [9] Лоскутов, А.Ю. Очарование хаоса / А.Ю. Лоскутов // Успехи физических наук. – 2010. - №12. – С.1305.
Web-Reference [10] Андронов, А.А. Теория колебаний / А.А. Андронов, А.А. Витт, С.Э. Хайкин. - М.: Государственное издательство физико-математической литературы, 1959. – 916с.
Web-Reference [11] Анищенко, В.С. Сложные колебания в простых системах / B.C. Анищенко. -М.: Наука, 1990. - 312с.
Web-Reference [12] Мигулин, В.В. Основы теории колебаний / В.В. Мигулин, В.И. Медведев, Е.Р. Мустель, В.Н. Парыгин. -М.: Наука, 1978. -392с.
Web-Reference [13] Анищенко, В.С. Знакомство с нелинейной динамикой / В.С. Анищенко. – Москва-Ижевск: Институт компьютерных исследований, 2002. – 144с.
Web-Reference [14] Анищенко, В.С. Лекции по нелинейной динамике / В.С. Анищенко, Т.Е. Вадивасова. -Саратов.: "Издательство Саратовского университета", 2010. -324с.
Web-Reference [15] Ландау, Л.Д. Механика / Л.Д. Ландау, Е.М. Лифшиц. -М.: Наука, 1988. -216с.
Web-Reference [16] Корн, Г. Справочник по математике / Г. Корн, Т. Корн. Пер. с англ.-М.: Наука, 1974. -832с.
Web-Reference [17] Novak, S. Transition to chaos in the Duffing oscillator /S. Novak, R.G. Frehlich // Physical review A. - 1982. -Vol.26. -№6. -P.3661
Web-Reference [18] Murali, K. Transmission of signals by synchronization in a chaotic Van der Pol-Duffing oscillator / K. Murali, M. Lakshmanan // Physical review E. -1993. -Vol.48. -№3. -P.47
Web-Reference [19] Van der Pol, B. On "relaxation-oscillations"/B. Van der Pol // Phylosophical Magazine and Journal of Science S7. -1926. -Vol.2. -№11. -P.978
Web-Reference [20] Van der Pol, B. Forced Oscillations in a Circuit with non-linear Resistance.(Reception with reactive Triode.) / B. Van der Pol // Phylosophical Magazine and Journal of Science S7. -1927. -Vol.3 -№13. -P.65
Web-Reference [21] Van der Pol, B. The heartbeat considered as a relaxation oscillation, and an electrical model of the heart/ B. Van der Pol, J. Van der Mark // Phylosophical Magazine and Journal of Science S7. -1928. -Vol.6. -№38. -P.763
Web-Reference [22] Ohm, G. Die galvanische Kette / G. S. Ohm. -Berlin.: Bei T.H. Riemann, 1827. -254p.
Web-Reference [23] Kirchhoff, G. Ueber den Durchgang eines elektrischen Stromes durch eine Ebene, insbesondere durch eine kreisformige/ G.R. Kirchhoff// Der Physik Und Chemie. - 1845. - №4. - BAND LXIV. - P.497
Web-Reference [24] Дженкинс, Г. Спектральный анализ и его приложения / Г. Дженкинс, Д. Ваттс. – М.: Мир, 1971. – 316с.
Web-Reference [25] Бендат, Дж. Прикладной анализ случайных данных / Дж. Бендат, А. Пирсол. – М.: Мир, 1989. –540с.
Web-Reference [26] Калиткин, Н.Н. Численные методы / Н.Н. Калиткин. – М.: Наука, 1978. – 512с.
Web-Reference [27] Турчак, Л.И. Основы численных методов / Л.И. Турчак, П.В. Плотников. - М.: Физматлит, 2005. –304с.